True RMS (Root-Mean-Square)
In electrical engineering, Root Mean Square, abbreviated as RMS, is a common mathematical calculation used to define the voltage or current of an AC waveform. The term is only applied to sinusoidal voltages, currents, or other complex waveforms and not in DC applications where the voltage is constant over time. It is defined as the square root of the mean square and is sometimes referred to as the quadratic mean.
RMS is a mathematical way to find the DC equivalent voltage of an AC waveform. This is a critical step in completing power calculations because using a simple average or a peak value would not properly calculate the effective value in an AC circuit. In other words, values that are labeled as RMS values may be used in power calculations whereas non-RMS values, such as peak values, will result in an inaccurate calculation for that system.
The following is an illustration of a pure sine wave. In this example, the peaks and valleys are symmetrical and follow a steady pattern. The peak value of this sine wave is 25 volts.
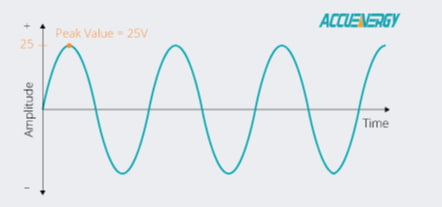
The formula to calculate RMS for a pure sine wave is as follows:
Vrms = 0.7071 x Vpeak
TUsing the peak value of 25 volts, the RMS value for the sine wave above can be calculated as:
Vrms = 0.7071 x 25V
Vrms = 17.68V
The value 17.68V can be used to complete power calculations on this system assuming this waveform remains constant. However, peak values are still an important variable must also be considered when sizing electrical systems. RMS values for perfect sine waves can be obtained by an averaging multimeter or power meter.
Measuring Non-Linear Loads
Pure sine waves can be easily measured using an averaging meter as the shape of the current waveform is proportional to the shape of the voltage waveform, resulting in an accurate RMS calculation.
What happens when the waveform is not a perfect sine wave? This is a common occurrence in the real world because much of the equipment in a modern facility will generate a non-linear load – that is, it will produce a waveform is not a pure sine wave and may fluctuate over time depending on load impendence and other factors.
These non-sinusoidal, non-linear waveforms have irregular patterns, may have spikes, or be angular in shape, such as square or triangular waves. They can be generated by common equipment such as variable speed fans, VFDs, electronics like computers or servers, LED lighting, telecommunications equipment, and more. Essentially, equipment that contains electronically programable, microprocessor-based components can create loads with current and voltage distortion that may cause the readings taken with an averaging meter to be underestimated by as much as 40% or over-estimated by up to 10%. This is because averaging meters are only using the Vpeak value for its calculation which is only accurate for pure sine waves.
Fortunately, there is a class of meter, known as a “true-RMS” (TRMS) meter, that is capable of accurately measuring non-linear loads. These meters employ a more sophisticated formula which uses samples across the waveform, delivering a more accurate result.
The true-RMS formula is as follows:
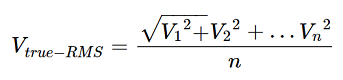
By taking many samples along the sinewave, a true-RMS meter can provide reliable measurements of a power system, regardless of the noise introduced by electronic devices connected to the system and can accurately display voltage and current waveforms. Be sure to deploy a true-RMS meter to maximize measurement accuracy at any facility.
